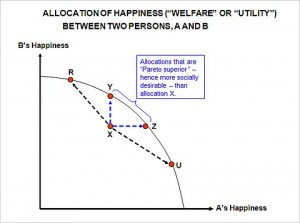
In today’s New York Times Economix Blog, Uwe Reinhardt poses the central question: “Is ‘More Efficient” Always Better?” In answer to the question he provides the basic definitions one would confront in an introductory economics course – including appropriate references to Pareto – and proceeds to point out that some efficient points, such as R and U, are not necessarily better than some inefficient ones (any in the region bounded by X, Y, and Z).
He then proceeds to link efficiency with optimality, which becomes his point of contention.
“One suspects that the term optimal came into widespread use among economists as a marketing device to promote their normative propositions based on efficiency. But as Professor Arrow warns his colleagues on this point:
A definition is just a definition, but when the definiendum is a word already in common use with highly favorable connotations, it is clear that we are really trying to be persuasive; we are implicitly recommending the achievement of optimal states.
Alas, it gets worse. Astute readers will have figured out by now that literally every point falling on the entire solid curve in the graph must be “Pareto optimal” by the economist’s definition of that term, not only those falling on line segment Y-Z. That circumstance makes the economist’s use of the word optimal even more dubious.”
In my view, Reinhardt stops in the wrong place. Rather than “dis” the term efficiency, he could differentiate between Pareto efficient (all points on the concave curve bounded by the two axes and called in this case the Happiness Possibility Frontier or HPF) and Pareto optimality (which employs Pareto’s notion that, at these points, to make someone better off, another person must be made worse off.) So what’s the point? Actually, there are two points to be made.
1. For any point (or allocation) below the HPF, that is any Pareto inefficient allocation, there exist Pareto improvement possibilities, and economists should encourage taking advantage of such.
2. Once on the HPF, Pareto optimal allocations depend upon social preferences, about which economists have no unique judgment to contribute; however, each such social choice judgment does yield consequences with opportunity costs (foregone choices) that can be identified. Stated differently, all Pareto efficient points are candidate points to be Pareto optimal under some set (of sometimes very curious) social preferences.
To conclude, the notion of efficiency is not a vague term, and it does reflect a value free standard. In my view, one can claim that for any Pareto inefficient allocation, Pareto improvements exist. Efficiency, however, says nothing about the optimal choice until preferences – in this case comparison of A’s vs. B’s happiness – is made. Furthermore, economists should encourage those making such social preferences to be transparent rather than hide them in 2000 pages of legislation.

