By Harsimran S. Kalsi

     Calabi-Yau Manifolds (CYMs) are incredibly intricate geometric structures which have several implications in mathematics and theoretical physics. In particular, CYMs have been utilized in contexts such as superstring theory and in explaining characteristics of higher dimensional spacetime.

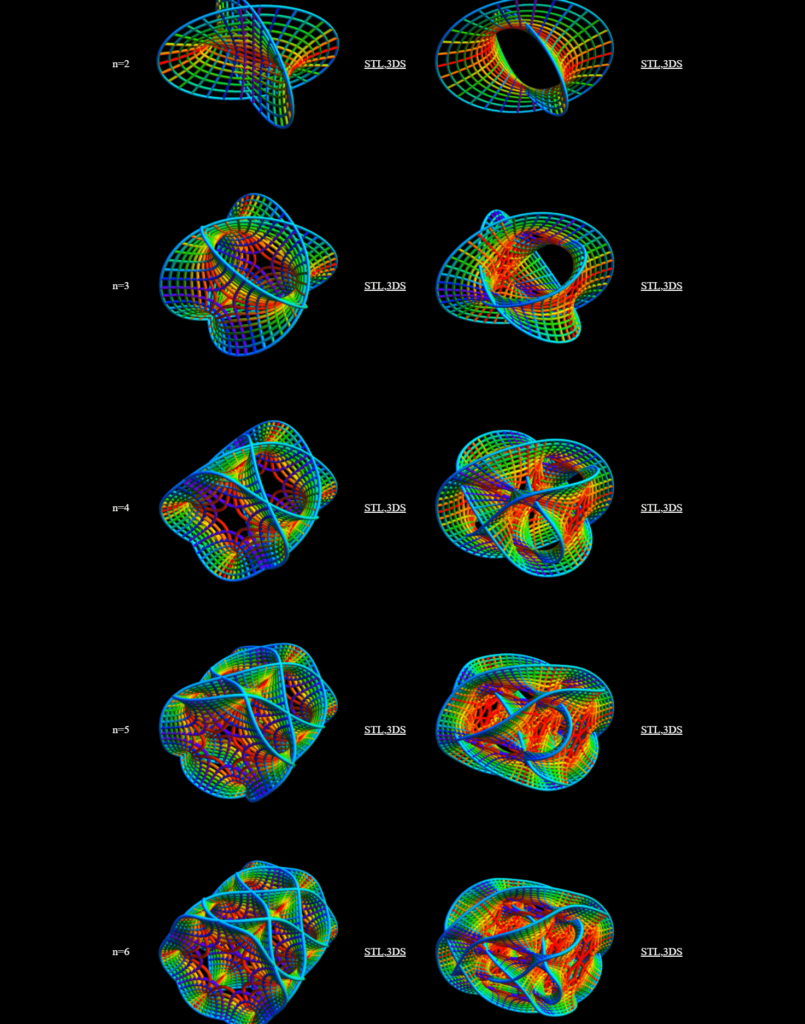
     In 2013, individuals at the Harvard Mathematics department created .stl files of various geometric shapes and published a very cool paper about using 3D printing technology to visualize mathematics. Knill and Slavkovsky stated that 3D printed representations of complex geometric objects/proofs could help promote understanding of the material.

     After some time, it occurred to me that the overall shape of a CYM vaguely resembles some aspects of a protein beta-barrel structure. My interest in 3D printing biochemically relevant objects (mixed with my urge to test the limits of economically feasible 3D printing) ultimately encouraged me to pursue printing some of these manifolds.

     Naturally, I decided to focus on printing the most complex manifolds first . . . both versions of the n=6 and n=7 manifolds (interestingly the n=2 and n=3 CYMs have been successfully printed previously: https://www.thingiverse.com/thing:165486) using PLA filament.

     When I initially started this project I saw some very promising results. I wanted to design the CYM file settings in such a way, that one could print the file without any supports whatsoever. Afterall, anytime a print can avoid support material is generally a good thing (conserve filament, reduce printing time, and easier to batch print).

     After what felt like dozens of failed prints I had almost become certain that printing a complicated structure like this without support was impossible.

     However, one day after making some final modifications to the size of the CYM and rotating its placement on the build plate (printing it horizontally–on its curves rather than vertically on its base) it was a success! The CYM printed without any supports and only required a raft! Upon further examination one could notice small frilly bits localized within the CYM but otherwise, the overall structure appeared to be high fidelity.

     Subsequently, I decided to continue playing around with various CYM files and parameters in addition to trying to replicate the support-free success. After several prints I found that the manifolds without the hole running through the middle were able to be printed on Ultimaker printers. I also found that the size of the CYM print had a huge impact on print success. It appeared that 45mm in length was the largest a print could get without becoming structurally compromised. This makes sense when one examines the internal structure of the CYM. Furthermore, it appeared that printing with supports connected to a raft, yielded the smoothest results.

     Using supports and a raft while rotating the print to be on its side, I was able to successfully print an n=7 CYM! A comparison of two CYMs can be seen below.

     In conclusion, these test prints and trials have been very informative to me about the limitations of certain CAD programs and of 3D printers located in the Makerspace. This information is ultimately incredibly useful, as I continue printing intricate and novel objects (e.g. certain proteins) in the future.

Acknowledgements: All .stl files obtained here were obtained through Elizabeth Slavkovsky’s and Oliver Knill’s work posted here: http://www.math.harvard.edu/~knill/3dprinter/exhibits/calabiyau/index.html. Special thanks to Angela Vanden Elzen for her support and assistance throughout this project. Additional thanks to Deron Brown for assisting me during experimental prints.

By Harsimran S. Kalsi

The human brain is arguably one of the most complex systems that humanity has ever come across. A three-pound mass of “jelly” with over 86 billion neuronal cells, all stowed away in the dark caverns of our skulls. This organ facilitates thinking, imagining, socially interacting, feeling, and so much more that can sometimes go unnoticed in our daily lives.

The intricacy and wonder of the human brain as well as its limitless potential as a target to enhance human health and wellbeing, are what drive my deep interest in the brain. I’ve long been fascinated by it ever since having first learned about Dr. David Eagleman’s work on creating new senses and Dr. Vilanyur S. Ramachandran’s and Dr. Oliver Sacks’ work on fascinating neurological cases.

Recently, I decided that I’d like to print a brain using files from the NIH 3D Print Exchange. In particular, I wanted to modify and print a file such that it highlights my favorite part of the brain–the frontal lobe. Of the four major lobes of the brain, it is the largest and is located just behind the forehead (at the front of both hemispheres). The frontal lobe is principally responsible for planning/thinking about the future, attention, motivation, and short-term memory (as well as some other features). In many ways, characteristics of our frontal lobes help define aspects of what it means to be human.

To “highlight” the frontal lobe I used the same method that I used previously to highlight distinct proteins on the surface of viruses. If you haven’t had a chance to read that post, you can find it here. In short summary, I used Meshmixer to divide the brain .stl into several distinct pieces and later merged them into specific groups, which could then be imported and manipulated in Cura (printing with an Ultimaker 3).

Overall, this process and print worked great! The prints came out fantastic and with a higher resolution of the sulci and gyri than I had initially anticipated. However, since I utilized the Meshmixer plane cut tool, the delineation of the frontal lobe from the other lobes is sometimes too sharp and a little off center. The frontal lobe is specifically separated from the parietal lobe by the Central Sulcus and separated from the temporal lobe by the lateral sulcus. This particular print does not show the frontal lobe in this much detail; however, it is a very close approximation (which appears to be off by ~1mm). Additionally, it is still useful from a “macro” educational and proof of concept perspective.

Acknowledgements:
The original .stl of the brain was obtained from the NIH 3D Print Exchange. Special thanks to Angela Vanden Elzen for her support and assistance throughout this project.