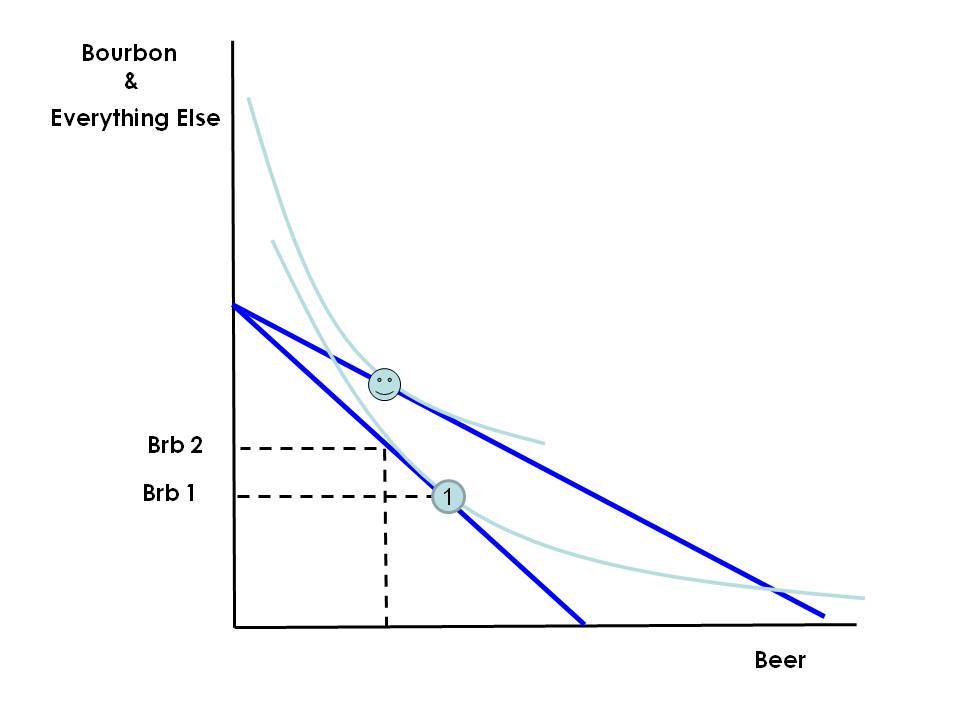
Professor Gerard has treated us again to some good, clean microeconomic fun. I think he is correct, and the bottom line is: if beer is a Giffen good, its consumption can fall as its price rises. His elaboration (and correction) of Yglesias is very nice, as is his translation of Yglesias’s argument into the neat graphical device of the iso-alcohol constraint. Yglesias’s original statement, however, that “…another possibility is that people hold total spending and total alcohol consumption [constant]…” strikes me as pretty sloppy, by Briggs 2nd floor standards. Why would one keep alcohol consumption constant, in the face of a price change? Changing circumstances leading to no change in a choice variable (alcohol consumption) is always suspicious, especially in a continuous model like this.
Yglesias seems to be groping (in the dark) for a characteristics model—in other words, a model where people care about characteristics (alcohol and taste) of goods, not the goods directly. This sort of model was thoroughly worked out in the 1970s, mainly by one famous Kelvin Lancaster. In this example, there are two goods, beer and bourbon, and they both have two characteristics (to various degrees), viz. alcohol and taste. The utility function is defined on alcohol and taste, and the quantities of characteristics consumed depend linearly on the quantities of beer and bourbon purchased. So, I thought, perhaps there is something interesting going on here. Maybe, just maybe, we could have a Giffen good even if the utility function (on characteristics) is perfectly normal, i.e., not Giffen. Luckily, before I got too absorbed in linear transformations, I took Google Scholar for a spin, and soon got to “A Contribution to the New Theory of Demand: A Rehabilitation of the Giffen Good” by Richard G. Lipsey and Gideon Rosenbluth, published in The Canadian Journal of Economics in 1971. Here is a taste from the Introduction:
Three of the most commonly used illustrations of possible Giffen effects are: Bread and meat, beer and whiskey, and Marshall’s account of transportation. There is a common feature of these three examples which “common sense” suggests is an essential requirement for a Giffen good and indeed for an inferior good, of which the Giffen good is a special case: there must be a “superior” good which shares one or more of the characteristics of the inferior good. If, for example, meat is substituted for bread as income rises, this implies that there is a want-satisfying characteristic shared by the two goods, in respect of which the substitution takes place. Bread must be a cheaper source of supply of this characteristic than meat, else the substitution would not depend on a rise in income. The reader can satisfy himself that similar reasoning applies to the other two examples.
They then go on to explain very neatly how Giffen goods could easily arise even if we assume that the utility function (on characteristics) excludes the possibility of a Giffen characteristic. Basically, if the income elasticity for characteristic 1 is very high compared to the income elasticity for characteristic 2, then an increase in real income will push the consumer to want so much more of characteristic 1, that just consuming more of the good that is more characteristic 1 intensive won’t do—he will have to cut back consumption of the other good to consumer even more of the good that is more characteristic 1 intensive. In our example, the income elasticity for taste is so much higher, that an increase in real income will push the consumer to want so much more taste that just buying more bourbon won’t do—he’ll have to cut back on beer and buy even more bourbon. However, as he does so, total alcohol consumption will still increase! (Remember, we assumed that there are no Giffen characteristics.)
I must say that I am pretty satisfied with the Lipsey–Rosenbluth explanation of why beer might be a Giffen good in this case. If the name Lipsey sounds familiar, that’s probably because of his association with The Theory of the Second Best, which probably requires a post of its own. (See also here.) And I would be remiss if I did not mention that Lipsey was a recipient of the 2006 Schumpeter award for the book Economic Transformations (co-written with two of his students).
I hereby propose that Griff’s Grill be renamed “Griffin Good” for a week in honor of economic science.